04_Probability distribution & estimation

Author

Yeong Chan Lee

Published

April 5, 2023

4-1. 확률분포

4강을 통해서 다양한 확률분포에 대해 배웠습니다. 여기서는 R을 통해 확률분포를 어떻게 표현할 수 있는지 알아보겠습니다.

정규분포

먼저 가장 와닿는 정규분포입니다.

정규분포는 아래와 같은 확률밀도함수를 갖습니다.

\[ X \sim N(\mu, \sigma^2) \]

\[ f_X(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{(x - \mu)^2}{2 \sigma^2}} \]

정규분포를 표현하는 기본 함수로 dnorm, pnorm, qnorm, rnorm이 있습니다. 이 때, 정규분포를 표현하기 위한 두 개의 파라미터는 무엇입니까? 평균과 표준편차(분산)입니다. 딱히 지정하지 않으면 기본값(default)은 평균은 0, 표준편차는 1입니다. ?dnorm 을 통해서 확인할 수 있습니다.

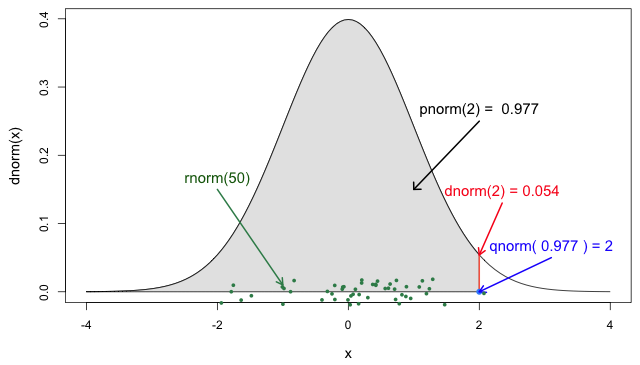
출처: Prof. Jack Weiss at UNC

출처: Prof. Jack Weiss at UNC

먼저 dnorm은 \(x\) 에 대한 density입니다. \(x\)의 범위는 \((-inf, inf)\)입니다. dnorm(1), dnorm(2) 등 다양하게 시도해보세요.

dnorm(0)
[1] 0.3989423
dnorm(1)
[1] 0.2419707
dnorm(2)
[1] 0.05399097
dnorm(-1)
[1] 0.2419707
dnorm(-2)
[1] 0.05399097

표준정규분포의 확률밀도함수를 직접 구현해볼까요?

x<-0
pdf_norm <- (1/sqrt(2*pi)) * exp(-1*(x^2/2))
print(pdf_norm)
[1] 0.3989423

표준정규분포는 0을 기준으로 대칭이기 때문에 dnorm(1)과 dnorm(-1)의 값이 같습니다. 그럼 이를 활용해서 그래프를 그려볼 수 있겠네요.

library(dplyr)

Attaching package: 'dplyr'
The following objects are masked from 'package:stats':

    filter, lag
The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union
library(ggplot2)

norm_df <- data.frame(X=seq(-3, 3, 0.1))
norm_df <- norm_df %>% mutate(Y = dnorm(X))

ggplot(data=norm_df, aes(x=X, y=Y)) +
  geom_line(size=2)
Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.

pnorm 함수는 \(P(X<x)\)와 대응합니다. 예를 들어 우리가 통계학에 배우게 되면 자주 보게 되는 1.96에 대해서 pnorm(1.96)이면\(P(X<1.96) \approx0.975\)가 됩니다.

pnorm(1.96)
[1] 0.9750021

반대로 qnorm은 확률이 \(P(X<x)\)가 될 때의 \(x\)가 무엇인지를 나타냅니다. 0.975가 들어가면 1.96에 근사하는 값이 나오겠네요.

qnorm(0.975)
[1] 1.959964

rnorm은 해당 정규분포에서 density를 랜덤하게 n개를 추출해줍니다. 그러니까 시뮬레이션 연구를 할 때 잘 쓰일 수 있겠습니다.

rnorm(10)
 [1]  1.69869894  0.02663649 -0.62638952 -0.23630300  0.10086453  1.00788479
 [7] -0.47044318 -0.30578876 -1.24955006  0.67224746

그러면 rnorm에서 랜덤값 1000개 정도 추출하고 histogram을 그리면 정규분포와 비슷하게 그릴 수 있겠네요. 이렇게 랜덤한 값들을 추출할 경우 추출값들이 그때 그때 달라지게 됩니다. 연구의 재현성(reproducibility)을 위해서 랜덤 추출값이 고정되게 나오게끔 set.seed()함수를 사용합니다.

set.seed(1234) #seed 값은 아무거나 들어가도 됩니다.
norm_df2 <- data.frame(Y=rnorm(1000))

ggplot(data=norm_df2, aes(x=Y)) +
  geom_histogram(binwidth=0.1)

이항분포

이렇게 각 분포들이 d, p, q, r을 앞에 붙여서 구현되어 있습니다. 우리는 각 분포들의 파라미터를 지정해주면 됩니다. 예를 들어 이항분포의 경우로는 dbinom, pbinom, qbinom, rbinom 이렇게 있습니다.

\[ P(X=k) = \binom{n}{k} p^k (1-p)^{n-k} \]

동전던지기를 10번 시행하는 경우로 예를 들어봅시다. 그러면 n은 10, p는 1/2가 되겠지요. 그 때 확률 변수 \(X\)의 범위는 0부터 10까지 될 것입니다.

binom_df <- data.frame(X=seq(0, 10, 1))
binom_df <- binom_df %>% mutate(Y = dbinom(X, size=10, prob=1/2))

ggplot(data=binom_df, aes(x=X, y=Y)) +
  geom_line(size=2) + 
  theme_light(base_size = 20)

The rule of five

\(B(n, p)\) 의 경우 \(npq \geq 5\)조건을 만족하면 \(N(np, np(1-p))\)로 근사될 수 있다고 배웠습니다.

\[ X \sim B(100,{1\over2}) \\ P(X \leq 50) \]

pbinom(q=50, size=100, prob=1/2)
[1] 0.5397946
pnorm(q=50+1/2, mean=100*1/2, sd=sqrt(100*1/2*1/2))
[1] 0.5398278

Normal approximation to the binomial distribution

N수가 증가하면 p에 관계 없이 정규분포로 근사하게 됩니다. 직접 다양하게 시도하면서 확인해보세요.

n <- 100
p <- 1/2
binom_df <- data.frame(X=seq(0, n, 1))
binom_df <- binom_df %>% mutate(Y = dbinom(X, size=n, prob=p))

norm_df <- data.frame(X=seq(0, n, 0.1))
norm_df <- norm_df %>% mutate(Y = dnorm(X, mean = n*p, sd = sqrt(n*p*(1-p))))

ggplot() +
  geom_line(data=binom_df, aes(x=X, y=Y, group=0), size=1, colour="red") + 
  geom_line(data=norm_df, aes(x=X, y=Y, group=1), linetype=2, size=1, colour="blue")+
  theme_light(base_size = 20)

중심극한정리

중심극한 정리에 따르면 모집단의 분포와 관계 없이 표본의 크기가 커질수록 표본 평균의 분포는 정규분포와 가까워집니다.

실제로 그렇게 되는지 확인해봅시다. 포아송 분포를 따르는 샘플을 랜덤하게 뽑은 후 이들의 평균이 정규분포를 따르게 되는지 시각적으로 확인합니다.

result <- c()
# 4. for문을 활용해 1000번정도 반복합시다.
for(n_trials in 1:1000){
  # 1. 평균이 10인 Poisson 분포에서 표본을 30개를 뽑습니다.
  my_sample <- rpois(n = 50, lambda = 10)
  
  # 2. 추출된 표본의 평균을 구합니다.
  my_mean <- mean(my_sample)
  
  # 3. 이를 데이터프레임에 저장합시다.
  tmp_df <- data.frame(NUM = n_trials, MEAN = my_mean)
  result <- rbind(result, tmp_df)
}

ggplot(data=result, aes(x=MEAN)) +
  geom_density() + 
  xlim(0, 20) +
  theme_light()

Bootstrap

어떤 통계량의 분포를 가정하지 않고 분포를 파악하고 싶을 때 쓸 수 있는 방법입니다. 내가 가진 표본 n개 샘플을 N번 무작위 복원 추출을 시행하여 나오는 N개의 통계량으로 분포를 확인할 수 있습니다. 이를 통해 Confidence interval을 그려볼 수 있습니다. 실험해보면 알겠지만 표본의 크기는 적당히 커야 합니다. n의 크기가 25 이상은 되어야 한다고 합니다. 1000과 같이 크게 해보세요. t.test 결과와 유사해집니다.

set.seed(1) #재현성을 위해 seed를 정합니다.

my_sample <- rnorm(50) # 우리가 가진 표본의 크기가 50이라고 합시다.

#분포를 가정하지 않고 평균의 분포가 궁금하다고 하면 bootstrap을 쓸 수 있습니다.
mean_vector <- c()
for(i in 1:1000){ # N은 보통 1000이상 지정합니다.
  boot_sample <- sample(my_sample, length(my_sample), replace = TRUE)
  mean_vector <- c(mean_vector, mean(boot_sample))
}

mean_vector <- sort(mean_vector)
print(paste0("bootstrap mean: ", round(mean(mean_vector), 3)))
[1] "bootstrap mean: 0.103"
print(paste0("95% bootstrap CI (", round(mean_vector[25], 3), ", ", round(mean_vector[975], 3), ")"))
[1] "95% bootstrap CI (-0.12, 0.312)"
t.test(my_sample)

    One Sample t-test

data:  my_sample
t = 0.85432, df = 49, p-value = 0.3971
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -0.1358313  0.3367278
sample estimates:
mean of x 
0.1004483

Bootstrap CI는 AUROC에 대한 신뢰구간을 구할 때 종종 쓰입니다. 추가로 AUROC에 대한 CI는 부트스트랩 말고 Delong’s test(DeLong, DeLong, and Clarke-Pearson 1988)를 활용할 수 있습니다 (pROC 패키지).

Poplin, R., Varadarajan, A.V., Blumer, K. et al. Prediction of cardiovascular risk factors from retinal fundus photographs via deep learning. Nat Biomed Eng 2, 158–164 (2018).

Poplin, R., Varadarajan, A.V., Blumer, K. et al. Prediction of cardiovascular risk factors from retinal fundus photographs via deep learning. Nat Biomed Eng 2, 158–164 (2018).

성균관대학교 삼성융합의과학원 의생명통계학 2023년 1학기 - 이영찬

References

DeLong, Elizabeth R., David M. DeLong, and Daniel L. Clarke-Pearson. 1988. “Comparing the Areas Under Two or More Correlated Receiver Operating Characteristic Curves: A Nonparametric Approach.” Biometrics 44 (3): 837. https://doi.org/10.2307/2531595.